Calculus

Limits:

A limit is one of the most important parts of calculus. The idea of a limit sets the foundation of everything in calculus such that every formal definition of a derivative and an integral is defined through a limit. So! What is a limit? A limit looks like this: \(\lim_{x \to 0} (3x+1)\) where the function $3x+1$ looks like this:

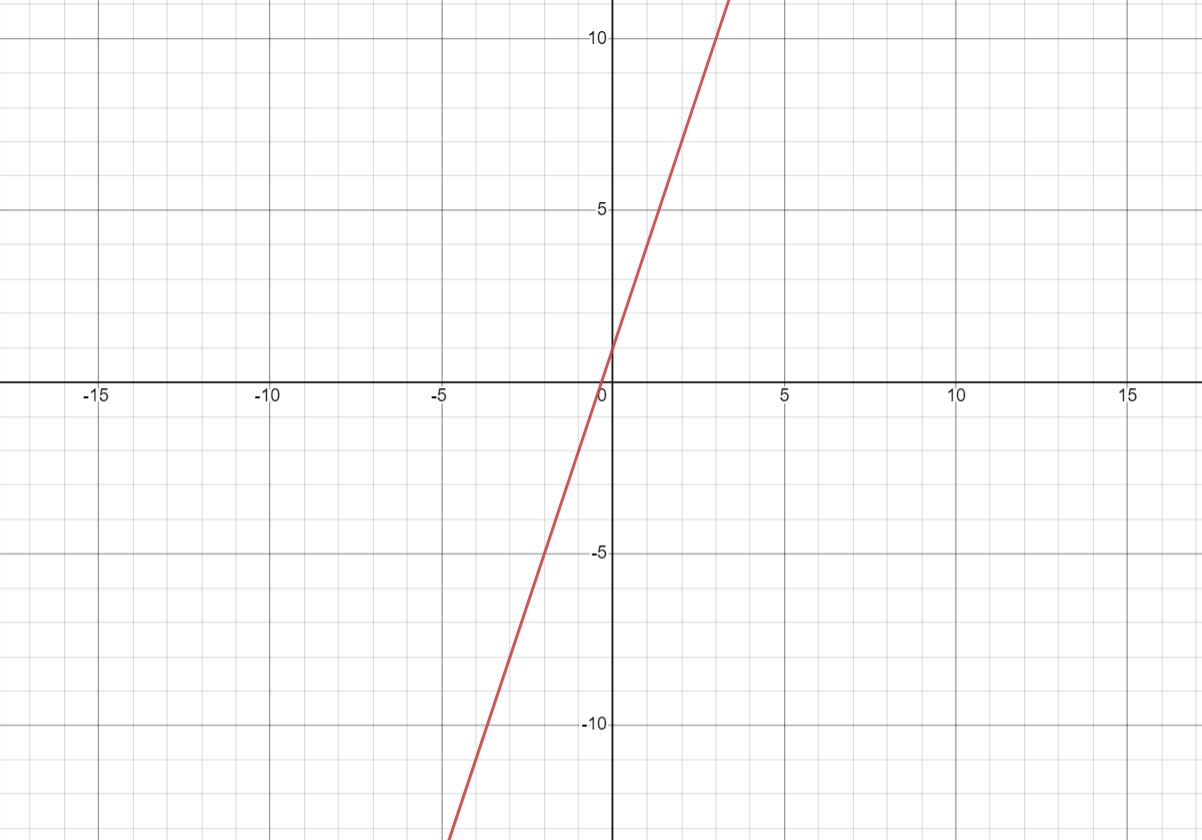
and what our limit is asking is this: as $x$ approaches $0$, what does the function $3x+1$ equal? Basically, if I zoomed in on this graph at $0$, what does the function equal? In this case:

\[\lim_{x \to 0} (3x+1)=1\]

This is the simple idea of a limit, and we use this definition to define the rest of calculus.

Diffentiation/Derivative:

A derivative is the instantaneous rate of change (can be visualized by the line tangent to the graph at a particular point) of a given function. Another way to think about it, the derivative is the SLOPE of the graph! For example: \(\frac{d}{dx}(2x)=2\) is the derivative of $2x$ with respect to $x$, and the answer $2$ is the slope/rate of change of $2x$ at all points on the function. This makes sense since the function $y=mx$ states that $m$ is the slope of the function $y$. Therefore, the slope/derivative of $y=2x$ is $2$. This understanding of a derivative generalizes to all functions! A function’s instantaneous rate of change at any point can be calculated through its derivative. Here are some differentation techniques that you will need to know:

1. Power Rule:

\[\frac{d}{dx}(x^n)=nx^{n-1}\]

1. Product Rule:

\[\frac{d}{dx}\Bigl(f(x)g(x)\Bigl)=f'(x)g(x)+f(x)g'(x)\]

1. Quotient Rule:

\[\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right)=\frac{g(x)f'(x)-g'(x)f(x)}{(g(x))^2}\]

1. Chain Rule (derivative of the inside multiplied by the derivative of the outside):

\[\frac{d}{dx}\Bigl[f(g(x))\Bigl]=f'(g(x))g'(x)\]

Common notation types for derivatives which are all equivalent, let $y=f(x)$:

\[\frac{dy}{dx}=\frac{d}{dx}(y)=\frac{df}{dx}=\frac{df(x)}{dx}=\frac{d}{dx}(f(x))\]

Derivative Analysis:

With derivatives, we can figure out a lot of interesting information about any particular function. Two important things we can learn about any function can be derived through its first and second derivatives. Take this function:

\[f(x)=x^3+x^2\]

And when graphed, looks like this:

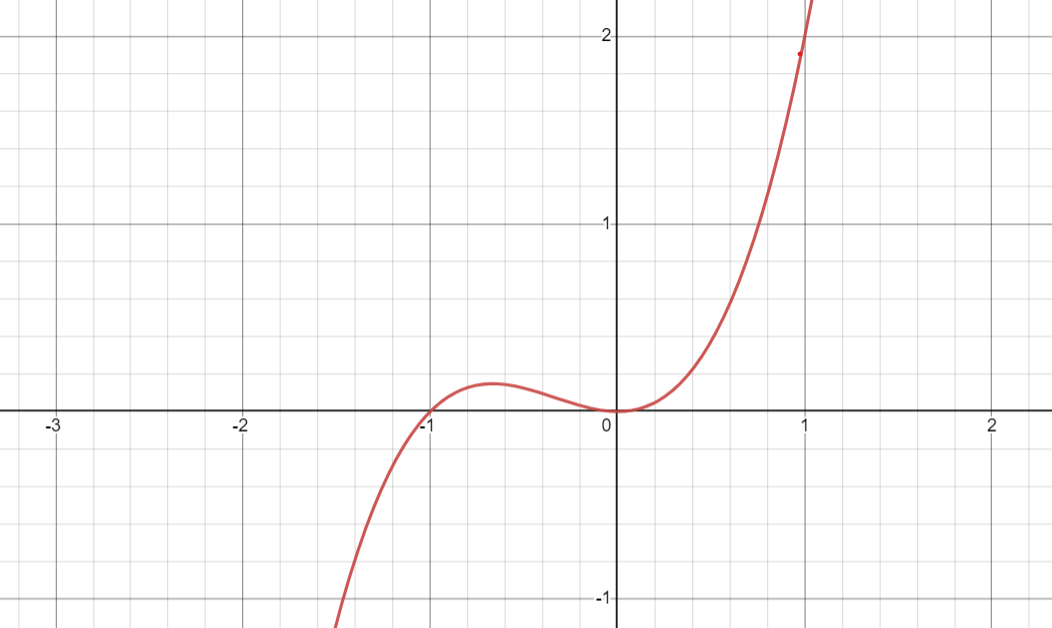
When you take the derivative of this function, what does the answer tell you? Well, we know that the first derivative tells us the slope of our graph. For example:

\[f(x)=x^3+x^2\rightarrow f'(x)=3x^2+2x\]

tells us that the slope of $f(x)$ is $3x^2+2x$ for all $x$. How about if we take the derivative again? Then, we have

\[f'(x)=3x^2+2x\rightarrow f''(x)=6x+2\]

which tells us that the slope of $f’(x)$ is $6x+2$ for all $x$. There are many different interesting things that we can learn about $f(x)$ given $f’(x)$ and $f’‘(x)$. Here are the various things you can learn from these new derivative functions:

• When the graph’s slope becomes zero! Do this through figuring out when $f’(x)=0$

• When does the graph go from positive slope to negative slope (also known as critical points)? Do this through the second derivative test. If $f’‘(x)>0$ when $f’(x)=0$, then the graph goes from a negative slope to a positive slope! If $f’‘(x)<0$ when $f’(x)=0$, then the graph goes from a positive slope to a negative slope.

• Is the graph concave up or down? Concave Up: $f’‘(x)>0$, Concave Down: $f’‘(x)<0$

Summation:

List of topics to include Below

1. Integration
   • Fundamental Theorem of Calculus
   • Integral Table
   • Polar Coordinates
   • Multiple Integration

Trigonometry

1. Logarithms
   • Logarithmic Formatting
     • $(\log_b n = a \textrm{ and } b^a = n)$
     • 
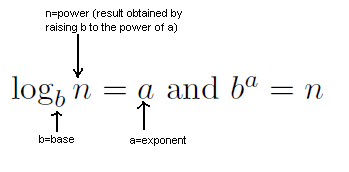
   • Natural Logarithms
   • Manipulation
   • Stirlings Approximation
2. Trigonometry Functions and Identities
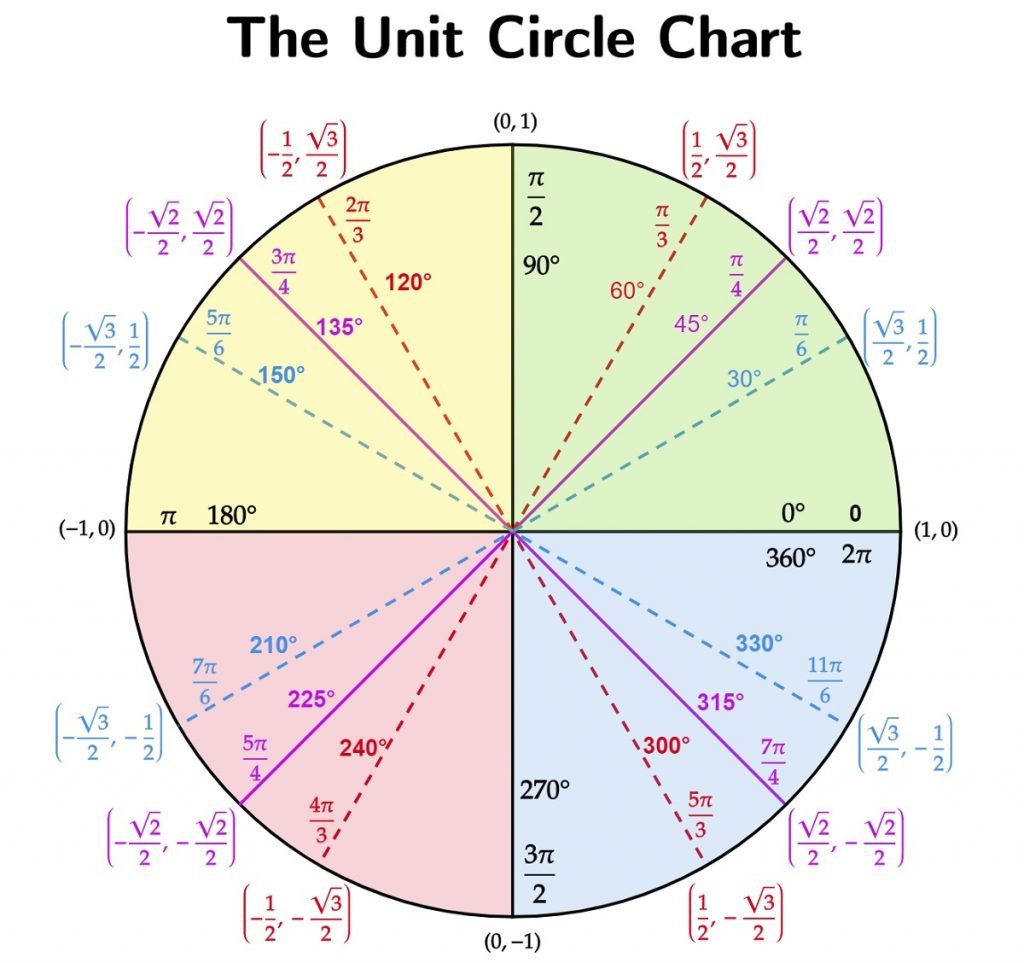
3. Unit Circle
   • 
4. Series and Series Expansions

Algebra

1. Multiplying One by One \(\frac{2+2}{4}\)
2. FOIL \((a+b)(c+d)\)
3. Deriving Equations
4. Solving a System of Equations

Linear Algebra

1. Eigen Functions
   • Eigen Function:
   • Eigen Value:
   • Eigen Vector:
2. Dot Product
3. Orthogonality
4. Determinants

Statistics

1. Normalization
2. Expectation Values
3. Standard Deviation
4. Variance
5. Mean, median, mode, etc.
6. Probability
7. Factorials

Additional Resources